Semaine 9

• Problème (publié le 28 octobre)

  Il est temps de travailler la géométrie et peut-être d'ajouter un outil à notre répertoire. Pour ce problème, un peu plus de connaissance en géométrie est nécessaire. Au besoin, googlez "la puissance d'un point".

  Un cercle $(O,r)$ et un point $A$ à l'extérieur du cercle sont donnés. À partir de $A$, on trace une droite $\epsilon$ distincte de $AO$ qui intersecte le cercle en $B$ et $\Gamma$, avec $B$ entre $A$ et $\Gamma$. Ensuite, on trace la réflexion de $\epsilon$ par rapport à l'axe $AO$ qui intersecte le cercle en $E$ et $\Delta$, avec $E$ entre $A$ et $\Delta$.

  Montrez que les diagonales du quadrilatère $B \Gamma \Delta E$ se croisent en un point donné, indépendant du choix de la droite $\epsilon$.

• Solution (publié le 4 novembre)

  Il s'agissait du problème 3 de la Compétition mathématique hellénique 2004 qui est apparu dans le Crux Mathematicorum [2007:336-337]. La solution proposée est de Pavlos Maragoudakis et fut donnée dans le Crux [2008:288].

  

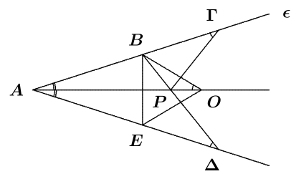
  Soit $AO \cap B\Delta = \{ P \} $. Par symétrie, $\angle A\Gamma P = \angle B \Delta A.$ Puisque $\angle B \Delta P = \frac{1}{2} \angle BOE = \angle BOA,$ on a $\angle A \Gamma P = \angle BOA.$ Ainsi, les triangles $ A \Gamma P$ et $ AOB$ sont semblables et $$ \frac{AP}{AB} = \frac{A \Gamma}{AO},$$ ou $AP = \frac{AB \circ A \Gamma}{AO}.$

  Comme $AB\circ A \Gamma = AO^2 - r^2,$ on a $AP = \frac{AO^2 -r^2}{AO},$ qui est indépendant de la droite $\epsilon.$ Par symétrie, $E \Gamma$ et $AO$ croisent aussi $P$ et la démonstration est terminée.

Semaine 8

• Problème (publié le 21 octobre)

  Cette semaine, un problème qu'il faut analyser en regardant des plus petites versions du même problème.

  On situe initialement dans la case au coin inférieur gauche d'un tableau $2 \times n$. On peut ensuite se déplacer sur une case adjacente, sans mouvements diagonaux et de façon à ce que chaque case soit visitée au plus une fois. De plus, deux cases faisant partie du chemin emprunté peuvent avoir un côté commun si et seulement si elles ont été visitées l'une après l'autre. On considère deux types de chemin: ceux qui se terminent à la case au coin supérieur droit et ceux qui se terminent à la case au coin inférieur droit. Le diagramme ci-dessous montre les $4$ chemins de chaque type lorsque $n = 4.$ Montrez que le nombre de chemins de chaque type est le même lorsque $n = 2014.$

  
• Solution (publié le 28 octobre)

  C'était le problème 5 de la deuxième partie 2 de l'édition 2013-2014 de la «Alberta High School Mathematics Competition». On donne la solution «officielle».

  Le chemin emprunté est uniquement déterminé par les mouvements verticaux. La seule restriction est que deux mouvements verticaux ne peuvent être faits dans des colonnes adjacentes. Le point d'arrivée du chemin (dans le coin inférieur droit ou supérieur droit) dépend donc seulement de la parité du nombre de mouvements verticaux. On représentent les colonnes par les éléments de l'ensemble $\{1,2,\ldots,n\}.$ On considère ensuite tout les sous-ensembles qui ne contiennent aucune paire de nombres consécutifs. Soit $a_n$, le nombre de tels sous-ensembles avec un nombre pair d'éléments, et $b_n$ le nombre de tels sous-ensembles avec un nombre impair d'éléments. On a $a_0 = a_1 = a_2 = 1$ à cause de l'ensemble vide, $b_0 = 0, b_1 =1$ et $b_2 =2.$ \newline

  Pour $n \geq 3$, on sépare les sous-ensembles de $\{1,2,\ldots,n\}$ en deux types: ceux qui contiennent $n-1$ et ceux qui ne contiennent pas $n-1$. Un sous-ensemble du premier type ne peut donc pas contenir $n-2$ ou $n.$ Ainsi, le nombre de sous-ensembles de ce type dont la cardinalité est paire est $b_{n-3}$ et le nombre de tels sous-ensembles avec un nombre d'éléments impair est $a_{n-3}.$ De leur côté, les sous-ensembles du deuxième type peuvent être arrangés en paire de façon à ce que dans chaque paire, les deux sous-ensembles soient identiques à la différence que le premier contient $n$ mais pas le second. Il y a donc autant de sous-ensembles de cardinalité paire que de sous-ensembles de cardinalité impaire dans ceux de deuxième type. On trouve donc que $a_n-b_n=b_{n-3}-a_{n-3}.$ Ainsi, $$a_{3k}-b_{3k} = (-1)^k(a_0-b_0) = (-1)^k,$$ $$a_{3k+1}-b_{3k+1} = (-1)^k (a_1-b_1)=0,$$ $$a_{3k+2}-b_{3k+2} = (-1)^k(a_2 -b_2) = (-1)^{k+1}.$$ En particulier, $a_{2014} = b_{2014}.$

Semaine 7

• Problème (publié le 14 octobre)

  Cette semaine, on propose un problème de géométrie qui ne nécessite que quelques résultats de base et de la trigonométrie.

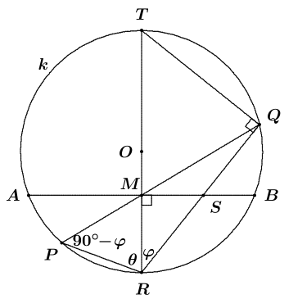
  Soit $k$ un cercle avec centre $O$ et $AB$ une corde de $k$ dont le point milieu $M$ esl distinct de $O.$ Le rayon du cercle qui passe par $M$ touche $k$ en $R.$ Soit $P$ un point sur l'arc mineur $AR$ de $k$, $Q$ l'intersection de $PM$ avec $k$ et $S$ l'intersection de $AB$ et $QR$. Quel segment est le plus long, $RS$ or $PM?$

• Solution (publié le 21 octobre)

  Il s'agissait du problème 5 de la première rondes des cours mathématiques spécialisés de l'Olympiade Mathématique de Hongrie 2005-2006. Ce problème fut donné dans le Crux Mathematicorum [2009:212]. La solution est de Geoffrey Kandall du Connecticut, États-Unis, et a été donnée dans le Crux [2010:282].

  Étendons $RO$ pour qu'il rejoigne $k$ en $T.$ On remarque que $\angle RMS$, $\angle RQT$ sont des angles droits.

  Soit $\angle MRP = \theta, \angle MRS = \phi.$ Alors $RM = RS \cos \phi$ et $ \angle RPQ = \angle RTQ = 90^\circ - \phi.$ Conséquemment, $$ \frac{PM}{\sin \theta} = \frac{RM}{\sin (90^\circ - \phi)} = \frac{RM}{\cos \phi } = RS ,$$ donc $PM = RS \sin \theta < RS.$

  

Semaine 6

• Problème (publié le 7 octobre)

  Cette semaine, on travaille avec des inégalités!

  Soit $p,q,$ et $r$ des nombres réels positifs et $n$ un entier supérieur ou égal à $1$. Si $pqr = 1$, montrez que $$ \frac{1}{p^n+q^n+1} + \frac{1}{q^n + r^n +1} + \frac{1}{r^n + p^n +1} \leq 1.$$

• Solution (publié le 14 octobre)

  C'était le problème 3 de la Compétition Mathématique «Baltic Way» de 2004 aussi donné dans le Crux Mathematicorum [2008:211-213]. La solution est de Titu Zvonaru, Roumanie, et est apparue dans le Crux [2009:150-151].

  Soit $p^n = x^3, q^n= y^3,$ et $r^n = z^3.$ On doit montrer que si $xyz =1$ alors $$ \frac{1}{x^3+y^3+1} + \frac{1}{y^3+z^3+1} +\frac{1}{z^3 + x^3 +1} \leq 1,$$ ou de façon équivalente, on doit montrer que $$ \frac{1}{x^3 + y^3 + xyz} + \frac{1}{y^3 + z^3 + xyz } + \frac{1}{z^3 +x^3 +xyz} \leq 1.$$ Puisque $x$ et $y$ sont positifs, $(x-y)^2(x+y) \geq 0$ et donc $(x-y)(x^2-y^2) \geq 0,$ ainsi $x^3 + y^3 \geq xy(x+y).$ On a donc que

  ${\large \begin{array}{llllll} & \frac{1}{x^3+y^3+xyz} & + & \frac{1}{y^3+z^3+xyz} & + & \frac{1}{z^3+y^3 +xyz} \newline \leq & \frac{1}{xy(x+y) +xyz} & + & \frac{1}{yz(y+z) +xyz} & + & \frac{1}{zx(z+x) + xyz} \newline = & \frac{x+y+z}{xyz(x+y+z)} & = & 1. & & \end{array} }$

  L'égalité tient si et seulement si $x=y=z=1$, ou si et seulement si $p=q=r=1.$

Semaine 5

• Problème (publié le 30 septembre)

  Cette semaine, on fait du dénombrement et on travaille avec des sommes.

  De combien de façons est-ce que le nombre $2000$ peut être écrit comme une somme de trois entiers strictement positifs pas nécessairement différents? (Des sommes comme $1+2+3$ et $3 +2 +1 $ sont considérées identiques.)
• Solution (publié le 7 octobre)

  C'était le problème 1 du Concours Mathématique Nordique et ce problème est apparu dans le Crux Mathematicorum [2003:435]. La solution est due à Michel Bataille de Rouen, France. Elle est apparue dans le Crux Mathematicorum [2004:381].

  On doit trouver le nombre de triplets $(n_1,n_2,n_3)$ d'entiers tels que $ 1 \leq n_1 \leq n_2 \leq n_3$ et $n_1 + n_2 + n_3 = 2000.$ Ce nombre est 333333, l'entier le plus près de $2000^2/12$, comme nous le montrerons bientôt.

  Plus généralement, soit $n$ un entier $n\geq 3$, et $t_n$ le nombre de triplets $(n_1,n_2,n_3)$ tels que $1 \leq n_1 \leq n_2 \leq n_3$ et $n_1+n_2+n_3 = n$. Pour $n \geq 2$, on dénote de manière similaire $d_n$ le nombre de paires $(n_1,n_2)$ telles que $1 \leq n_1 \leq n_2$ et $n_1 + n_2 =n.$

  Il est clair que $d_2 = d_3 = 1$ et plus généralement, on voit que $d_n = n/2$ si $n$ est pair et $d_n = (n-1)/2$ si $n$ est impair. Pour $t_n$, on trouve que $t_3 = t_4 = 1$ et $t_5 =2.$ Pour $n \geq 6$, on a la relation $t_n = d_{n-1} +t_{n-3}$ puisqu'il y a $d_{n-1}$ triplets pour lesquels $n_1 =1$ et que l'ensemble des triplets pour lesquels $n_1 \geq 2$ est en bijection avec l'ensemble des triplets $(n_1-1,n_2-1,n_3-1)$ dont la somme des entrées est $n-3.$

  Maintenant, supposons que $n = 6k +2$ pour un certain entier positif $k$. Alors $$\begin{array}{ccc} t_n & = & (t_{6k+2}-t_{6k-1})+ (t_{6k-1} -t_{6k-4}) + \cdots \newline & & +(t_{11}-t_8) + (t_8 -t_5) +t_5 \newline & = & d_{6k+1} + d_{6k-2} + d_{6k-5} + \cdots + d_7 + d_5 \newline & = & 3k +(3k-1) + (3k -3) + (3k-4) + \cdots + 6 + 5 + 3 + 2 \newline & = & \frac{k(3k+1)}{2} + \frac{k(3k+1)}{2} = k(3k+2) = \frac{n^2}{12} - \frac{1}{3}, \end{array}$$ qui est l'entier le plus près de $n^2/12.$ Pour $n=2000$ ceci nous donne $t_n = 333333.$ (En traitant les cas $n=6k, 6k+1,6k+3, 6k+4, 6k+5$ de la même façon, il est facile de montrer que $t_n$ est toujours l'entier le plus près de $n^2/12$).

Semaine 4

• Problème (publié le 23 septembre)

  Cette semaine, on étudie ce qu'on appelle une équation fonctionnelle.

  Trouvez toutes les fonctions $f : \mathbb {R} \rightarrow {\mathbb R}$ telles que $$ f(xf(x) + f(y)) = x^2 +y$$ pour tout $x \in \mathbb {R}$ et $y \in \mathbb{R}.$

• Solution (publié le 30 septembre)

  Il s'agissait du problème 6 de la 11ème Olympiade Mathématique d'Ukraine. La question a aussi été proposée dans le Crux Mathematicorum [2006:217-218]. La solution de Li Zhou du Polk Community College est apparue dans le Crux Mathematicorum [2007:228].

  Il est facile de vérifier que $f(x) = x$ et $f(x) = -x$ satisfont l'équation fonctionnelle. On va montrer qu'il s'agit des seules solutions.

  Soit $f$ une solution à l'équation. En posant $x=0$ dans l'équation fonctionnelle, on trouve $f(f(y)) = y$ pour tout $y \in \mathbb {R}.$ Donc, pour tout $x, y \in \mathbb {R},$ $$x^2+y = f(xf(x)+f(y)) = f(f(x)f(f(x)) + f(y)) = f(x)^2 +y.$$ Ainsi, $f(x)^2 = x^2$ pour tout $x \in \mathbb{R}$. Si $f(1)=1$, alors $$ 1+2x+x^2 = f(1+x)^2 =f(1f(1) + f(f(x)))^2$$ $$ = (1^2 +f(x))^2 = 1 +2f(x) +x^2,$$ et donc $f(x) = x$ pour tout $x \in \mathbb{R}.$

  De la même façon, si $f(1)= -1$, alors $$ 1-2x+x^2 = f(-1+x)^2 = f(1f(1) + f(f(x)))^2$$ $$ = (1^2 +f(x))^2 = 1 + 2f(x) +x^2,$$ et donc $f(x) = -x$ pour tout $ x \in \mathbb{R}.$

Semaine 3

• Problème (publié le 16 septembre)

  Cette semaine, le problème proposé tire ses origines de l'algèbre enseignée au niveau secondaire.

  Soit $x,y,$ et $z$ des nombres réels tels que $\begin{array}{ccc} x+y+z =3 & \mbox{et} & xy + yz + xz = a \end{array}$, où $a$ est une constante réelle. Déterminez la valeur de la constante $a$ pour laquelle la différence entre la valeur maximale et minimale de $x$ vaut $8.$

• Solution (publié le 23 septembre)

  C'était le problème 1 de la 7ème Olympiade nationale de Bosnie-Herzegovine en 2002, aussi proposé dans le Crux Mathematicorum [2005:436]. La solution est de Pierre Bornsztein, de Maisons-Laffitte, France. Elle est apparue dans le Crux Mathematicorum [2007:22].

  On a que $y+z = 3-x$ et donc $yz = a -x(3-x).$ Il est facile de vérifier que le système $$\begin{array}{ccc} y+z & = & s \newline yz & = & p \end{array}$$ avec des inconnues $y$ et $z$, a une solution réelle si et seulement si $s^2 -4p \geq 0.$

  Ainsi, la seule condition à vérifier pour qu'il y ait une solution est $(3-x)^2 \geq 4(a-3x + x^2),$ qu'on réécrit $3(x-1)^2 \leq 4(3-a).$ Il est donc nécessaire que $a\leq 3$ et on a $$1-2 \sqrt{1 - \frac{1}{3}a} \leq x \leq 1 + 2 \sqrt{1 \ \frac{1}{3}a}.$$ La différence entre la valeur maximale et minimale pour $x$ vaut $8$ si et seulement si $4\sqrt{1-\frac{1}{3}a} = 8,$ ce qui implique que $a = -9.$

Semaine 2

• Problème (publié le 9 septembre)

  Un certain temps est nécessaire pour trouver comment aborder le problème!

  Deux voitures sont à 100 mètres de distance et voyagent dans le même sens sur une route à la vitesse limite de 60 km/h. À un certain moment, la vitesse limite augmente à 80 km/h. Plus tard, celle-ci augmente à 100 km/h. Un peu plus loin, la limite augmente à 120 km/h. Lorsqu'une voiture arrive à un panneau de changement de vitesse, celle-ci change immédiatement de vitesse pour prendre la vitesse limite. Lorsque les deux voitures avancent simultanément à 120 km/h, à quelle distance sont-elles l'une de l'autre?

• Solution (publié le 16 septembre)

  Il s'agissait du problème 3 de la deuxième partie de l'édition 2013-2014 du «Alberta High School Prize Examination».

  Supposons que la première voiture est au point $B$ pendant que la deuxième voiture est au point $A$, deux points dans la zone de 60 km/h. Alors $AB = 100$ mètres. Supposons que la première voiture est au point $D$ pendant que la deuxième voiture est au point $C$, deux points dans la zone de 120 km/h. Le temps que prends la deuxième voiture pour passer du point $A$ au point $C$ est le même que pour passer du point $B$ au point $D$. Les deux voitures prennent le même temps pour passer du point $B$ au point $C$. Ainsi, le temps que prend la deuxième voiture pour passer du point $A$ au point $B$ à 60 km/h est égal au temps que prends la première voiture pour passer du point $C$ au point $D$ à 120 km/h. On trouve donc que $CD =2 AB = 200$ mètres.

Semaine 1

• Problème (publié le 2 septembre)

  Deux problèmes sont proposés pour la première semaine. Le premier est un puzzle et aucune démarche n’est demandée. Dans le deuxième, on traitera de divisibilité et des chiffres qui com- posent l’écriture d’un nombre. Pour celui-ci, vous devrez justifier votre solution.

  Problème A
  Dans une maison, il y a un certain nombre de poissons, d’oiseaux et de chats. Au total il y a 15 têtes et 14 pattes. S’il y a plus d’un animal de chaque type dans la maison, combien y a-t-il de poissons?

  Problème B
  On place 2014 chiffres en ligne. Toute paire de chiffre adjacents dans la ligne forment un nombre divisible par 17 ou 23.

  1. Si le dernier chiffre de la ligne est un 1, quelle valeur peut prendre le premier chiffre de la ligne?
  2. Si le premier chiffre de la ligne est un 9, quelle valeur peut prendre le dernier chiffre de la ligne?
• Solution (publié le 9 septembre)

  Problème A
  [ Il s’agit du problème A6 de l’édition 2014 du Concours de mathématiques junior de Calgary.]
  On pose $P$ comme le nombre de poissons, $O$ pour le nombre d'oiseaux et $C$ comme le nombre de chats. La condition des pattes nous donne $2O +4C =14$, donc $O + 2C =7$. La condition des têtes nous donne $P+O+C = 15$. Comme il y a au moins deux animaux de chaque type, il y a au moins deux chats. Il ne peut y avoir plus de 2 chats, donc $C=2$ et $O=3$. On trouve ainsi que $P = 15-2-3 =10.$

  Problème B
  [ Il s’agit du problème B2 de l’édition 2014 du Concours de mathématiques junior de Calgary. ]
  

  1. Les nombres à deux chiffres qui sont multiples de $17$ sont $17,\ 34, \ 51, \ 68 $ et $85.$ Les multiples de $23$ sont $23,\ 46,\ 69$ et $92.$ On peut ensuite travailler à partir du premier chiffre connu pour déterminer la valeur de celui qui le précède dans la ligne. On commence avec la paire $x1$ et la seule possibilité pour $x$ est $5$. Ceci nous donne que $51$ termine la ligne. Avec $x5$ on trouve $851$, puis $6851$, $46851$,$346851$, $2346851$,$92346851$ et $692346851$. Il est ensuite clair que la séquence $92346$ de longueur $5$ se répètera. Puisque $2014 = 402 \times 5 + 4$, il y aura $402$ blocs de $69234$ suivis de $6851$. Le premier chiffre de la ligne est donc un $6.$
  2. On utilise la même méthode en travaillant cette fois du début vers la fin de la ligne. Le $9y$ nous force à ce que $92$ débute la ligne, puis on trouve $923$, $9234$ et $92346$. À ce point, il y a deux candidats possibles: un multiple de $17$, soit $68$ et un multiple de $23$, soit $69$. Traitons tout d'abord le cas où la ligne se poursuit avec $68$, i.e la séquence initiale à partir du début est $923468$. On trouve ensuite $9234685$, $92346851$ et $923468517$. À ce point, nous sommes bloqués puisqu'il n'y a aucun nombre de la forme $7y$ dans nos listes. On traite ensuite le cas où $69$ poursuit la séquence. Comme dans la partie a), on remarque que dans ce cas le cycle $92346$ de longueur $5$ est formé. On remarque finalement qu'il y a deux possibilités différentes pour la ligne. Le premier consiste en $402$ blocs de $92346$ terminés par $8517$ et l'autre consiste en $402$ blocs de $92346$ terminés par $9234$. Les deux possibilités pour le dernier chiffre de la ligne sont $4$ et $7.$