Le Défi ouvert canadien de mathématiques 2017 — nov. 2/3

Nicolae Strungaru
Problème de la semaine
— Nicolae Strungaru, Grant MacEwan University
Les problèmes du DOCM se divisent en trois parties. Pour la partie A, il n'est pas nécessaire d'écrire ses démarches dans la solution. Il est même possible de résoudre les problèmes sans avoir à écrire quoi que ce soit. Les problèmes de la partie B présentent un défi plus élevé et nécessitent des connaissances un peu plus poussées. Pour ceux-ci, vous aurez sans doute besoin de papier et d'un crayon. Les problèmes de la partie C nécessitent des réponses complètes avec justification pour les arguments proposés.
Nous avons sélectionné une variété de problèmes provenant de divers concours nationaux et régionaux avec l'espoir de susciter votre intérêt pour la résolution de problèmes et vous donner un peu de préparation pour le Défi ouvert canadien de mathématiques en novembre. Les problèmes touchent à large éventail de domaines mathématiques (algèbre, logique, géométrie...) mais ne sont pas associés à un âge scolaire précis.
Nous publierons les solutions aux problèmes la semaine suivante. Nous avertissons toutefois les enseignants qu’il se pourrait que des étudiants déterminés trouvent les solutions ailleurs en ligne avant qu’elles ne soient publiées ici.
Pour obtenir d’autres ensembles de problèmes et de solutions à chacun de ces niveaux, n’hésitez pas à télécharger les anciens examens officiels et leurs solutions dans nos archives.
Semaine 9
-
Problème
(publié le
31 octobre)
L'aire d'un trapèze est de 2 cm$^2$ et la somme des longueurs de ses diagonales est de $4$ cm. Déterminez la hauteur du trapèze.
-
Solution
(publié le
7 novembre)
Il s'agit du problème 4 de l'Olympiade mathématique de Géorgie 1997, apparu dans le Crux Mathematicorum [2000:193]. On donne la solution de Amengual Covas modifiée par l'éditeur pour publication dans le Crux Mathematicorum [2002:204-205].
On débute en montrant que les diagonales sont égales et perpendiculaires en $O$.
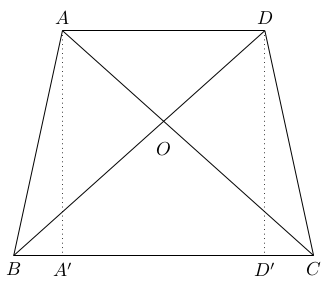
We first prove that the diagonals are equal and perpendicular at $O$.
On a \begin{align} \mbox{Area} (ABD) &= \frac{1}{2} BD \cdot AO \cdot \sin(\angle AOB) \cr \mbox{Area} (CBD) &= \frac{1}{2} BD \cdot CO \cdot \sin(\angle COD) \cr 2=\mbox{Area} (ABCD) &= \frac{1}{2} BD \cdot AC \cdot \sin(\angle AOB) \cr \end{align}
Posons $BD=x$. Alors $AC=4-x$ et donc $$4= x (4-x) \sin(\angle AOB) \leq x(4-x) =4x-x^2=4-(x-2)^2 \leq 4 \,.$$
Ainsi, toutes les inégalités de la ligne précédente sont des égalités. Ceci implique que \begin{align} 4-(x-2)^2 &= 4 \qquad \mbox{and} \cr x (4-x) \sin(\angle AOB) &= x(4-x). \cr \end{align}
La première égalité nous donne $x=2$ et donc $BD=x=2=4-x=AC$. La deuxième égalité nous donne $\angle AOB=90^\circ$ et donc $AC \perp BD$.
Pour continuer, nous montrons que $AB=CD$ et donc que le trapèze est isocèle. Pour le voir, on trace les perpendiculaires au segment $BC$ passant par $A$ et $D$ et on les nomme respectivement $AA'$ et $DD'$.
On a alors \begin{align} AC &=BD \cr AA' &= DD' \cr \angle AA'C & =\angle DD'B= 90^\circ \cr \end{align}
Ceci implique que les triangles rectangles $AA'C$ et $DD'B$ sont congrus et donc que $A'C=BD'$. On en déduit que $$A'B=CD' \,.$$
Les triangles rectangles $AA'B$ et $DD'C$ sont congrus puisque \begin{align} A'B &= D'C \cr AA' &= DD' \cr \angle AA'B & =\angle DD'C= 90^\circ \cr \end{align} et donc $AB=CD$.
Comme $ABCD$ est un trapèze isocèle, on en déduit que $BOC$ est un triangle rectangle isocèle, et donc $\angle OCB=45^\circ$. On trouve alors $AA'=A'C$.
Finalement, \begin{align} 2 &= \mbox{area}(ABCD) = \mbox{area}(ABA')+ \mbox{area}(AA'D'D)+ \mbox{area}(CDD') \cr &= \mbox{area}(AA'D'D)+ 2\mbox{area}(CDD') \cr &= AA' \cdot A'D'+ DD' \cdot D'C= AA'\cdot A'C \cr \end{align}
Puisque $AA'=A'C$ on a que $A'A^2=2$ et donc $$AA'=\sqrt{2} \,.$$
Semaine 8
-
Problème
(publié le
24 octobre)
Un triangle aigu $ABC$ est inscrit dans un cercle de centre $O$. La bissectrice de $\angle A$ croise le segment $BC$ en $D$. La perpendiculaire à $AO$ passant par $D$ croise la droite $AC$ en un point $P$ situé entre $A$ et $C$. Montrez que $AB=AP$.
-
Solution
(publié le
31 octobre)
Il s'agit du problème 5 de l'Olympiade mathématique d'Italie de 1995, apparu dans le Crux Mathematicorum [1998:323-324]. On donne ici la solution de Pierre Bornsztein, publiée dans le Crux Mathematicorum [2000:79-80].
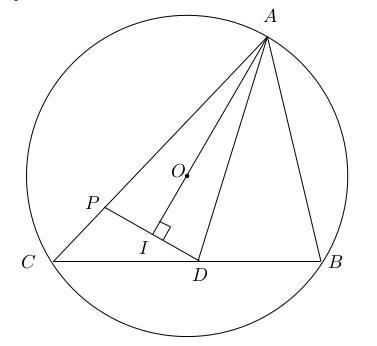
Puisque $ABC$ est aigu, $O$ est située à l'intérieur de $ABC$. Puisque $P$ est sur le segment $AC$, $O$ est situé à l'intérieur de $ADC$.
On notera $\angle A= \alpha, \angle B= \beta$ et $\angle C= \gamma$. On a ainsi \begin{align} \angle AOC &= 2 \beta \cr AO&=OC \cr \end{align} et donc $$\angle CAO = \frac{1}{2} ( 180^\circ -2 \beta) =90^\circ - \beta \,.$$
Ceci nous donne $$\angle OAD = \frac{\alpha}{2}-\left(90^\circ - \beta \right)=\frac{\alpha}{2} +\beta -90^\circ \,.$$
Nommons $I$ l'intersection de $AO$ et $PD$. Le triangle $\Delta AID$ est rectangle en $I$ et donc \begin{align} \angle PDA &=\angle IDA = 90^\circ - \angle OAD \cr &=180^\circ - \frac{\alpha}{2}-\beta \cr &=180^\circ - \angle DAB -\angle DBA =\angle ADB \,.\cr \end{align}
Ainsi, nous avons \begin{align} \angle PDA &=\angle ADB \cr AD &=AD \cr \angle PAD &= \angle BAD \cr \end{align}
Ceci nous montre que les triangles $\Delta PDA$ et $\Delta BDA$ sont congrus, et donc $PA=BA$.
Semaine 7
-
Problème
(publié le
17 octobre)
Existe-t-il un nombre $q \in \mathbb N$ et un nombre premier $p \in \mathbb N$ tel que $$3^p+7^p = 2 \cdot 5^q?$$
-
Solution
(publié le
24 octobre)
Il s'agit du problème 4 des Olympiades mathématiques Ukrainiennes de 11e année, apparu dans le Crux Mathematicorum [2006:217-218]. On donne la solution de Michel Bataille publiée dans le Crux Mathematicorum [2007:227-228].
Il n'existe aucune paire $(p,q)$ qui répond aux conditions. Pour le démontrer, on procède par contradiction.
Considérons qu'une telle paire $(p,q)$ existe. On vérifie rapidement que le cas $p=2$ est impossible. Ainsi, $p$ est impair et donc $$2 \cdot 5^q=3^p+7^p=10 \cdot (3^{p-1}-3^{p-2}\cdot 7+...-3 \cdot 5^{p-2}+7^{p-1}) \,.$$
On en déduit que \begin{align} 3^{p-1}-3^{p-2}\cdot 7+...-3 \cdot 7^{p-2}+7^{p-1}&=5^{q-1} \tag{1}\cr \end{align}
Quelques calculs nous confirment que $q=1$ ne satisfait pas aux conditions initiales, donc $5^{q-1} \equiv 0 \pmod{5}$. En utilisant le fait que $3\equiv -2 \pmod{5}$, que $7\equiv 2 \pmod{5}$, et que $p$ est impair dans (1), on trouve $$2^{p-1}+2^{p-1}+...+2^{p-1}=p2^{p-1} \equiv 0 \pmod{5} \,.$$
Ceci implique que $p=5$ et donc que $$2 \cdot 5^2 \cdot 341=3^5+7^5 = 2 \cdot 5^q \,,$$ ce qui est une contradiction.
Semaine 6
-
Problème
(publié le
10 octobre)
Le problème de cette semaine implique 2 polynômes.
Soit $P(X)$ et $Q(X)$ deux polynômes à coefficients entiers. Si $\frac{P(n)}{Q(n)}$ est entier pour tout entier $n$, montrez qu'il existe un polynôme $S(X)$ à coefficients rationnels tel que $P(X)=Q(X)S(X)$.
-
Solution
(publié le
17 octobre)
Il s'agit du problème 5 de la partie B du «Alberta High School Math Competition 1995» On présente la solution officielle.
En divisant $P(X)$ par $Q(X)$, on obtient le quotient $S(X)$ et le reste $R(X)$. Autrement dit, $$P(X)=Q(X)S(X)+R(X) \,,$$ où $\deg(R(X)) < \deg(Q(X))$. Ainsi,~: \begin{align} \frac{P(X)}{Q(X)}&= S(X)+ \frac{R(X)}{Q(X)} \,.\tag{1}\cr \end{align}
Puisque $P(X)$ et $Q(X)$ ont tous deux des coefficients entiers, $S(X)$ doit avoir des coefficients rationnels. Pour compléter la démonstration, on doit montrer que $R(X)=0$.
On peut écrire $$S(X)=\frac{1}{m} T(X) \,,$$ pour un certain entier $m > 0$ et un certain polynôme à coefficients entiers. En combinant l'hypothèse avec (1), on obtient que pour tous les entiers $n$, on a $$m \frac{R(n)}{Q(n)} = m\frac{P(n)}{Q(n)}-T(n) \in \mathbb Z \,.$$
Puisque $\deg(Q(x)) > \deg(R(x))$, pour une valeur $x$ assez grande on a $$\left| m \frac{R(x)}{Q(x)} \right| < 1 \,.$$
Ainsi, pour tous les entiers $n$ assez grands, on sait que $\left| m \frac{R(n)}{Q(n)} \right|=0$ et donc que $R(n)=0$. Ceci montre que $R$ a une infinité de racines et donc que $R=0$.
Note de l'éditeur~: Remarquons qu'on ne peut pas conclure que $S(x)$ a des coefficients entiers. Par exemple, si $P(X)=X^2+X$ et $Q(X)=2$ alors $\frac{P(n)}{Q(n)}=\frac{n(n+1)}{2}$ est un entier pour tous les entiers $n$ mais $S(X)=\frac{1}{2}X^2+\frac{1}{2}$.
Pólya a démontré qu'un polynôme $P(X)$ prend des valeurs entières à toutes les valeurs entières si et seulement s'il existe un $n$ et des entiers $a_0,..,a_n$ tel que \begin{align} P(X)&= a_n \frac{X(X-1)...(X-n+1)}{n!}+a_{n-1} \frac{X(X-1)+...+(X-n+2)}{(n-1)!}+...\cr &+a_{2} \frac{X(X-1)}{2!}+a_1X+a_0 \,.\cr \end{align}
Êtes-vous en mesure de démontrer ce résultat?
Semaine 5
-
Problème
(publié le
3 octobre)
La suite $a_n$ est définie par $a_1=1$ et par la relation suivante valide pour $n \geq 1$ : $$ a_{n+1}=\frac{a_n}{1+n a_n} \,. $$
Déterminez la valeur de $a_{1996}$.
-
Solution
(publié le
10 octobre)
Il s'agit du problème 5 de l'édition 1999 du Íslenzka Staerŏfræŏikeppni Framhaldsskólanema, apparu dans le Crux Mathematicorum [2001:232-233]. On donne la solution de Michel Bataille, publiée dans le Crux Mathematicorum [2003:304].
On remarque que $a_n >0$ pour tous les $n$. Donc pour tout $n$ nous avons $$ \frac{1}{a_{n+1}}=\frac{1}{a_n}+n \,. $$
Ainsi, $$ \begin{align} \frac{1}{a_{1996}}-1 &= \frac{1}{a_{1996}}-\frac{1}{a_1}= \sum_{k=1}^{1995} \left( \frac{1}{a_{k+1}}-\frac{1}{a_k} \right) \cr &= \sum_{k=1}^{1995} k =\frac{1995 \cdot 1996}{2} =1991010. \cr \end{align} $$
Conséquemment, $$a_{1996}=\frac{1}{1991011} \,.$$
Semaine 4
-
Problème
(publié le
26 septembre)
Trouvez tous les polynômes $P(X)$ qui satisfont $$(X-16)P(2X)=16(X-1)P(X).$$
-
Solution
(publié le
3 octobre)
Il s'agit du problème 3 de la 10e édition de l'Olympiade mathématique d'Irlande (1997) qui est apparu dans le Crux Mathematicorum [2001:6-8]. La solution a été publiée dans le Crux Mathematicorum [2003:96]. Voici une solution alternative de celle déjà publiée.
En posant $X=16$ dans l'équation, on obtient $P(16)=0$ et ainsi, on peut écrire $P(X)=(X-16)P_1(X)$ pour un certain polynôme $P_1(X)$. La relation devient alors $$(X-8)P_1(2X)=8(X-1)P_1(X) \,.$$
En posant $X=8$, on obtient $P_1(8)=0$ et ainsi on peut écrire $P_1(X)=(X-8)P_2(X)$ pour un certain polynôme $P_2(X)$. La relation devient ensuite $$(X-4)P_2(2X)=4(X-1)P_2(X) \,.$$
En posant $X=4$, on obtient $P_2(4)=0$ et ainsi on peut écrire $P_2(X)=(X-4)P_3(X)$ pour un certain polynôme $P_3(X)$. La relation devient $$(X-2)P_3(2X)=2(X-1)P_3(X) \,.$$
En posant $X=2$, on obtient $P_3(2)=0$ et ainsi on peut écrire $P_3(X)=(X-2)P_4(X)$ pour un certain polynôme $P_4(X)$. La relation devient $$P_4(2X)=P_4(X) \,.$$
On trouve alors que $P_4(1)=P_4(2)=P_4(4)=P_4(8)=...=P_4(2^n)=..$. Le seul choix est donc que $P_4(X)=a$ pour une certaine constante $a$.
Réponse : $P(X)=a(X-16)(X-8)(X-4)(X-2)$.
Semaine 3
-
Problème
(publié le
19 septembre)
Cette semaine, le problème porte sur un point à l'intérieur d'un carré.
Un point $E$ situé dans un carré $ABCD$ est tel que $AE=5, BE=2\sqrt{2}$ et $CE=3$. Déterminez l'aire du carré $ABCD$.
-
Solution
(publié le
26 septembre)
Il s'agit du problème 3 de la partie B du «Alberta High School Math Competition 2002». On présente la solution du participant Keith Chung.
On trace les perpendiculaires $EF$ et $EG$ de $E$ vers les côtés $AB$ et $AC$ respectivement.
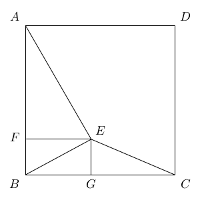
Posons $$ \begin{align} EF & = x \cr EG & =y \cr AB & =s. \end{align} $$
Ainsi, $$ \begin{align} x^2+y^2&=8 \tag{1}\cr (s-x)^2+y^2&=9 \tag{2}\cr x^2+(s-y)^2&=25 \tag{3} \end{align} $$
À partir de (1) et (2), on obtient $s^2-2sx=1$ et donc $$x=\frac{s^2-1}{2s}.$$
À partir de (1) et (3), on obtient $s^2-2sy=17$ et donc $$x=\frac{s^2-17}{2s}.$$
En substituant dans (1) on trouve $$(s^2-1)^2+(s^2-17)^2=32s^2,$$ qui peut être réécrite sous la forme $$(s^2-5)(s^2-29)=0.$$
Puisque $E$ est à l'intérieur de $ABCD$ et que $AE=5$, il est impossible que $s=\sqrt{5}$. Donc $s^2=29$ et l'aire recherchée est 29.
Semaine 2
-
Problème
(publié le
12 septembre)
Cette semaine, on s'intéresse à une équation aux racines entières.
Trouvez tous les nombres rationnels $r$ pour lesquels toutes les solutions à l'équation $$ rx^2+(r+1)x+r-1=0 $$ sont entières.
-
Solution
(publié le
19 septembre)
Il s'agit du Problème 5 de la ronde finale de la $21^{\mbox{e}}$ Olympiade mathématique Autrichienne, 1990, publiée dans le Crux Mathematicorum [1992:100]. On présente les solutions semblables de Joseph Ling, Pavlos Maragoudakis et Michael Selby, apparues dans l'édition [1993:138].
Si $r=0$, alors l'équation devient $x-1=0$, donc $x=1$. Ainsi $r=0$ est une solution.
Si $r \neq 0$, posons alors $x_1 \leq x_2$ les solutions à l'équation quadratique. Alors $$ \begin{align} x_1+x_2 &= -\frac{r+1}{r}=-1-\frac{1}{r} \cr x_1x_2 &= \frac{r-1}{r}=1-\frac{1}{r} \,. \end{align} $$
Ainsi $$ \begin{align} x_1x_2-(x_1+x_2) &= 2 \cr (x_1-1)(x_2-1) &= 3 \,. \end{align} $$
Si $x_1 \leq x_2$ sont des entiers, on a soit $x_1=2, x_2=4$ ou $x_1=-2, x_2=0$.
Dans le premier cas, on obtient $r=-\frac{1}{7}$ tandis que dans le second, $r=1$.
Réponse : $r \in \{ -\frac{1}{7}, 0, 1 \}$.
Semaine 1
-
Problème
(publié le
5 septembre)
Nous débutons avec deux problèmes d'introduction cette semaine.
Problème A
Démontrez que le nombre $$ \underbrace{111...111}_{1997}\underbrace{222...222}_{1998}5 $$ est un carré parfait.Problème B
Dans la figure, $ABCD$ est un rectangle avec $AD=1$. Les segments $BF$ et $DE$ sont tous deux perpendiculaires à la diagonale $AC$. De plus, $AE=EF=FC$. Déterminez la mesure de $AB$.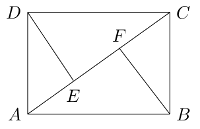
-
Solution
(publié le
12 septembre)
Problème A
Il s'agit du problème 1 de la 2e Olympiade mathématique junior Balkane (1998) qui est apparu dans le «Skoliad Corner» du Crux Mathematicorum [2002:522]. On donne la solution officielle présentée dans l'édition [2003:262].
$$ \begin{align} \underbrace{111...111}_{1997}\underbrace{222...222}_{1998}5 &=\underbrace{111...111}_{1997}\underbrace{000...000}_{1999}+2\cdot \underbrace{111...111}_{1998}0+5 \cr & = \frac{10^{1997}-1}{9}\cdot10^{1999}+2 \cdot \frac{10^{1998}-1}{9}\cdot10+5\cr & =\frac{1}{9} \left(10^{3996}-10^{1999}+2\cdot10^{1999}-20+45 \right) \cr & =\frac{1}{9} \left(10^{3996}+\cdot10^{1999}+25 \right) \cr & =\frac{1}{9} \left(10^{3996}+2 \cdot 5 \cdot10^{1998}+5^2 \right) \cr & =\frac{1}{9} \left(10^{1998}+5 \right)^2 =\left(\frac{10^{1998}+5}{3}\right)^2=\left(\frac{10^{1998}-1}{3}+2\right)^2 \cr &=\left( \underbrace{333...333}_{1998}+2 \right)^2 \end{align} $$
Problème B
Il s'agit du problème 10 de la finale junior du «British Columbia Secondary School Mathematics Contest» de 2008, apparu dans le «Skoliad Corner» du Crux Mathematicorum [2008:321-324]. Nous présentons la solution de Jixuan Wang qui a été publiée dans l'édition [2009:269].
Soit $x$ la mesure commune de $AE, EF$ et $FC$. Alors $EC=2x$.
Par le théorème de Pythagore, $AE^2+DE^2=AD^2$ et donc $$DE=\sqrt{1-x^2} \,.$$
Remarquons que $$\angle ECD =90^\circ -\angle EDC =\angle ADE \,,$$ ainsi $$\Delta DEA \sim \Delta CED \,.$$
On obtient alors $$ \begin{align} \frac{EA}{DE} &=\frac{ED}{CE} \qquad \Rightarrow \cr \frac{x}{\sqrt{1-x^2}} &= \frac{\sqrt{1-x^2}}{2x} \qquad \Rightarrow \cr 2x^2&=1-x^2 \qquad \Rightarrow \cr x&=\frac{1}{\sqrt{3}} \end{align} $$
Ainsi, $AC=3x =\sqrt{3}$ et par le théorème de Pythagore avec $\Delta ABC$ on obtient $$AB= \sqrt{2} \,.$$
Pour signaler des erreurs ou des faits manquants pour cette page, veuillez communiquer avec nous au docm@smc.math.ca.
